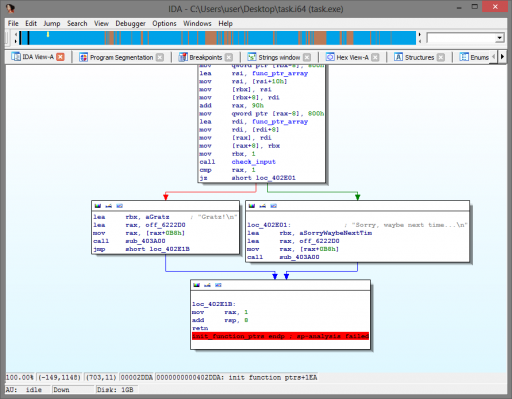
We are given a file, “task.exe,” and told that “smthg wrong with this env.” Running `file` tells us that this is not an EXE at all: it is an x86_64 ELF. We try to run it and quickly determine it expects a certain command-line argument. After digging around in IDA Pro, we find the branch where the program decides whether the input is valid.
Reversing this program is made frustrating by the fact that it was written in OCaml, generating many instructions that maintain internal structures, check stack alignment, etc. Learning to spot this extraneous code and skip over it takes time. Further reversing shows that the program creates an array of function pointers and calls each in turn, feeding in data based on the command-line argument(s). After each function call within this list, the return code is checked and the program fails if the function returns 1. It becomes clear that in order to get the flag, we must pass the checks performed by each function within this list.
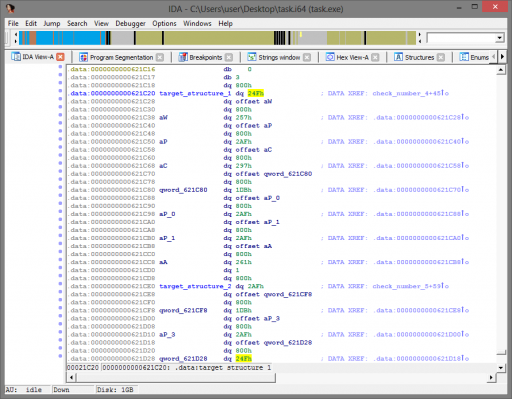
The purpose of the first of these functions is easy to determine: they only return success if there is one command-line argument of length 16. After this point, I began looking for shortcuts due to time, and eventually came upon some static data that is compared to a similar-looking, generated list based on our input.
By changing the command-line argument slightly, we can determine that this structure is an array comprised of eight values, where each value depends on a combination of two characters in our sixteen-character input. By changing only one character at a time from a string of “0000000000000000,” we determine exactly how each value is generated.  The rest of the functions mentioned earlier check the values within this array (and another array that is similarly generated) against our input and return success if our input matches. This challenge is now reduced to simply finding input that will generate values to match this array! The final algorithm is determined to be (where [n] denotes the ASCII value of the character at position n, counting from 1):
| Index | Target value | Formula |
|---|---|---|
| 0 | 0x24f |
[02]*2+[14]*4+1 |
| 1 | 0x257 |
[13]*2+[12]*4+1 |
| 2 | 0x2af |
[09]*2+[08]*4+1 |
| 3 | 0x297 |
[07]*2+[03]*4+1 |
| 4 | 0x1db |
[10]*2+[06]*4+1 |
| 5 | 0x2af |
[16]*2+[05]*4+1 |
| 6 | 0x2af |
[15]*2+[04]*4+1 |
| 7 | 0x261 |
[01]*2+[11]*4+1 |
Had the formula been more complicated, I would certainly not have figured this out, since I determined this via linear algebra by changing the input string. You’ll notice that the above formulae actually allow for many different combinations of ASCII values. For instance, index 0 can be satisfied by the combination of either ‘e‘ and ‘a‘, or by ‘K‘ and ‘n‘. The last few functions within the function pointer array, as mentioned earlier, check a second array, which limits these possibilities. Here is the algorithm for that second array:
| Index | Target value | Formula |
|---|---|---|
| 0 | 0x91 |
[01]*2+1 |
| 1 | 0xc3 |
[14]*2+1 |
| 2 | 0xe9 |
[12]*2+1 |
| 3 | 0xe5 |
[08]*2+1 |
| 4 | 0xdd |
[03]*2+1 |
| 5 | 0x89 |
[06]*2+1 |
| 6 | 0xf3 |
[05]*2+1 |
| 7 | 0xe5 |
[04]*2+1 |
| 8 | 0xe9 |
[11]*2+1 |
This second array gives enough information to completely determine the expected string; simple math gives us the solution.
Flag: HenryDorsettCase